二項モデルとは、オプション評価方法においてブラックショールズモデルと並ぶ代表的な方法。
オプションの権利行使期間を細分化して株価を上昇と下落の場合分けし、将来の株価の推移を予測して現在のオプションの価値（プレミアム）を推定する方法です。場合分けの図示が枝状に分岐してゆくことから「ツリーモデル」、あるいは全体図が格子状になるところから「格子モデル」とも呼ばれています。
オプション価格は原資産価格の動きに付随しているので、将来の原資産価格がわかれば、そこから逆算して現在のオプション価格が求められるというものです。
目次
試験では2通り
試験での出題は、ツリー表示によって3期間経過後の損益から、オプションの期待値を求めるものです。また、最近では1回だけ”差分モデル”とよばれる、具体的な事例に基づいてオプションの価値を評価する手法についての出題がありました。
理解しておきたい要点は以下の通りです。
- コールオプション（買う権利）の保有者（買い手）
取引価格が上昇することに価値がある。
当初約束した”安い価格”で取引可能である（安く買える）ため。 - プットオプション（売る権利）の保有者（買い手）
取引価格が下落することに価値がある。
当初約束した”高い価格”で取引可能である（高く売れる）ため。
この際、期待される（値上がりまたは値下がり）状態の加重平均のみ求めます。詳しくは下記の解答例を見ればわかると思います。また、プラスやマイナスにとらわれず絶対値（変化幅）だけで評価することも忘れずに。
差分モデルの場合には、利益と損失で相殺して求めます。
2021年第2回（問題42）の解答
プットオプションの買い手（2項モデル）の場合の期待値は、値下がり時の加重平均。
2021年第1回（問題43）の解答
コールオプションの買い手（2項モデル）の場合の期待値は、値上がり時の加重平均。
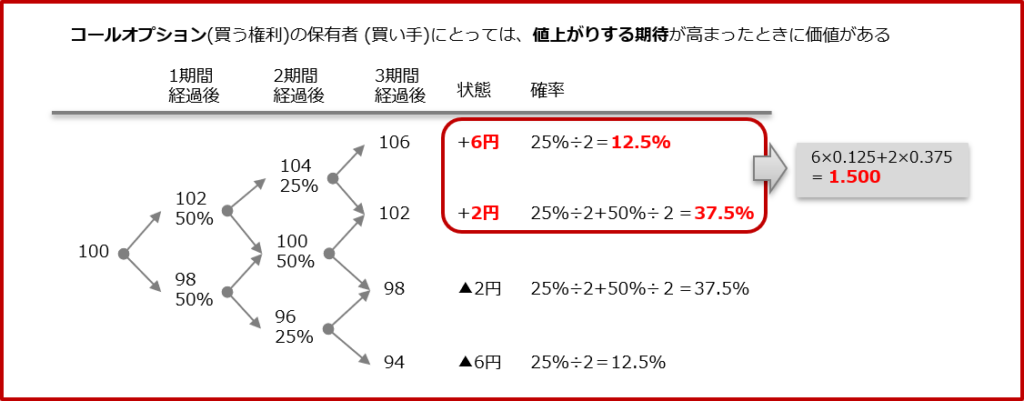
2020年第2回（問題42）の解答
プットオプションの買い手（2項モデル）の場合の期待値は、値下がり時の加重平均。
2019年第2回（問題42）の解答
コールオプションの買い手（2項モデル）の場合の期待値は、値上がり時の加重平均。
2019年第1回（問題44）の解答
コールオプションの買い手（差分モデル）の場合の期待値は、差分の加重平均。
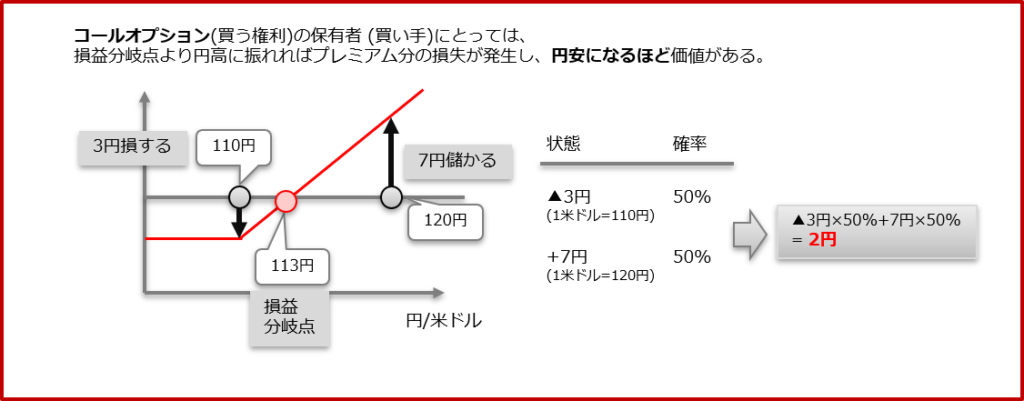
2018年第1回（問題41）の解答
コールオプションの買い手（2項モデル）の場合の期待値は、値上がり時の加重平均。
■合格したいあなたへ（各課目の要点解説）
金融｜不動産｜ライフ｜リスク｜タックス｜相続
■試験対策(2024年第1回試験向け)
最新版オリジナルテキスト(購入)｜テキスト訂正事項｜受験対策講座
■CFP®試験・金融資産運用について
・金融資産運用に合格したいあなたへ
・試験分析/金融 2021年 第1回 第2回
・試験分析/金融 2022年 第1回 第2回
・試験分析/金融 2023年 第1回 第2回
